The other day I was walking and thinking a categorical cross-entropy. We use it all the time in large language models, nobody even questions it for classification nowadays. However, is this a good way to do things? It seems like a big waste of space, since we have to one hot all the vectors, so we have to have a lookup table for of the size of the vocabulary.

Also, in the end the loss itself is just and inner product of the one hot encoded vector with the log prob vector, which exactly recovers the formula.

This seems like such a waste of space. You just one hot encode the stuff, that inner product just takes out that one probability. All of the rest is for nothing. That is kinda bad. Why not use the space we have in $n$ dimensions more effecitnently? For example consider the space of 3 dimensions, if we one hot encode into it, we place the 3 classes onto the axes. But there is so much more space in between! And on the other side of all the planes! No need to actually use another dimension! Look at the picture.

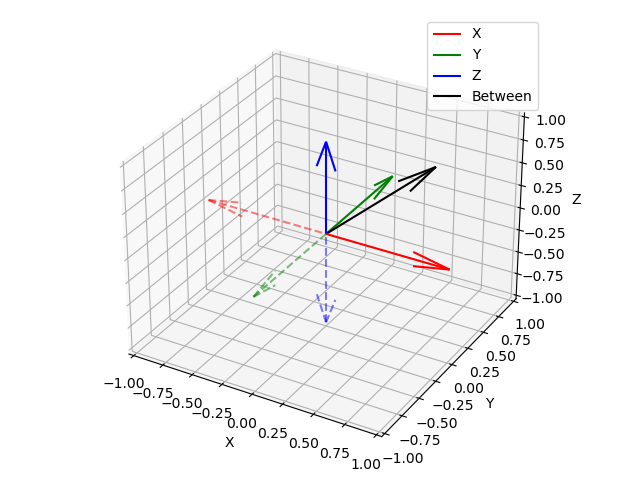
I decided to see if I can do this differently. For illustrative purposes, here I have chosen the MNIST problem. I am doing this on my personal laptop, and I do not have a GPU, so it goes pretty slow. MNIST has 10 classes and just cause it is nice to visualize, I decided to solve it in 3 dimensions.

Optimal Vectors

So how do we do this? How do we find the best vectors for our space? We want vectors that are as distinct as possible from each other, however still fit into a small amount of dimensions. We are interested in predicting normalized vectors, since what interest us is the direction not the magnitude. Therefore our problem is:

How to obtain $k$ unit vectors in $n$ dimensions such that they are aligned the least possible?

This is called the Thompson’s Problem, which was first defined on electrons and their repelling forces. There does not seem to be a closed solution for general $n$ and $k$, so we can solve this using optimization (SGD!).

Here we could have this as trying to minimize the maximum of $X_{ij} =\langle x_i, x_j \rangle$ for pairs of vectors $x_i$, $x_j$. But we can also just relax this problem and minimize the $\sum_{i,j} X_{ij}$. Gemini suggested even using the exponential to use exponential to incentivize minimization, hence $\sum_{ij} \exp(X_{ij})$. Once these vectors are found, they are fixed and we can learn to predict in alignment with those, using cosine similarity as a loss function, I call it WarpedCrossEntropy. Here you can see an example of optimized vectors.

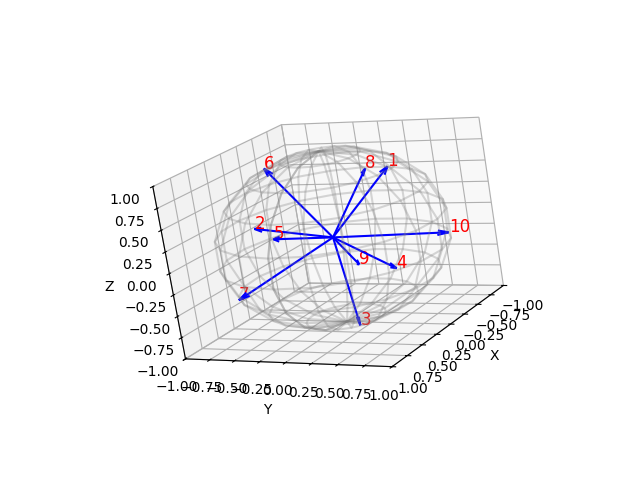
To test this idea out, and I decided to compare this to normal CrossEntropy and see if I can outperform it.

Results

Long story short, I took one layer MLP with ReLU, the size of the latent space is 64 and then I project onto 10 classes and train using normal CrossEntropyLoss. For WarpedCrossEntropy, I project only onto 3 dimensions. Here are the loss training curves.

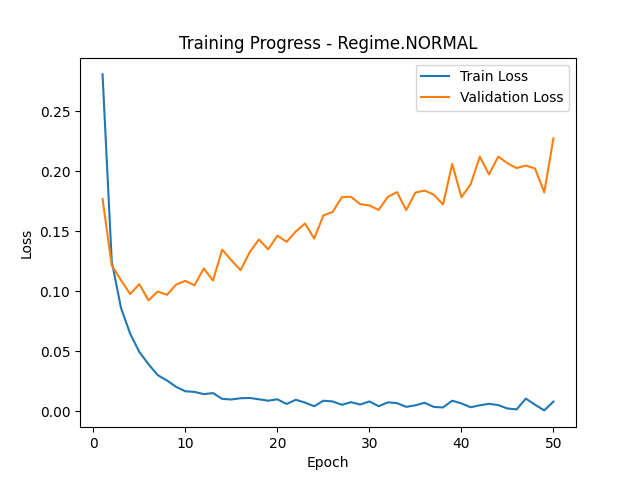
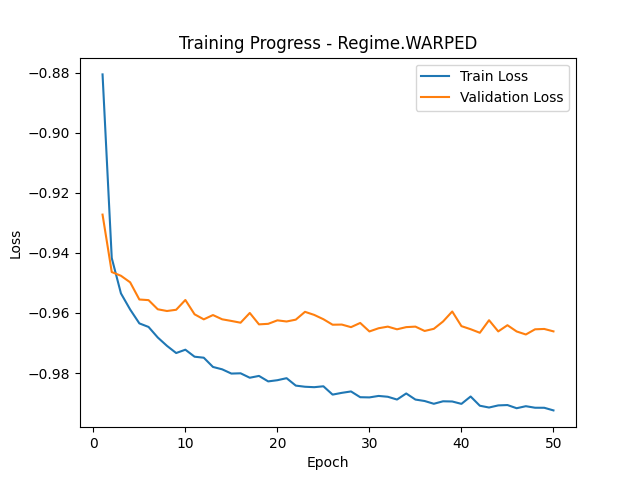
We can see, that the training with WarpedCrossEntropy takes a lot more time. Also the losses are not really comparable in magnitude. However, they both seem to be training. Finally, I have compared the performance of those runs on test data by looking at the closest vector in label class.

Well, honestly, not too bad! It seems that the methods works! Actual parameter reduction is very small, we only get some on the final layer, but we have to train those before we fixed them, so it does not really make that much sense.

Learnings & Discarded Ideas

One thing I wanted to try was normalization: I did not notice that under the hood torch CrossEntropy does softmax on the inputs, and I thought it is trained just as is. However, this is not the case. Equivalently, I was thinking I could unnormalize the vectors in my WarpedCrossEntropy. However, it seems the softmax is there for a reason as otherwise the training does not stabilize.

I wanted to also do a joint optimization: starts with random vectors on a unit sphere, and then learn the classes while learning the optimimal positions. However, that did not really work as the MLP is good enough in learning just any set of random vectors and does not really optimize them after a while. I tried to encourage it with scaling the loss, or enlarging the gradient, but no succees. The vectors would not move. I also tried creating a loss which would repell repel vectors of other classes from the one of the correcly predicted class, but the training did not stabilize.

Future Directions

Main thing I would like to figure out if you can actually make use of this in high-dimensional settings: let’s say we are learning on 100000+ classes (e.g. language modelling). Will projection from a tight latent space onto such class space difficult? Could WarpedCrossEntropy help there?

Secondly, I would like to compare this to encoding classes using binary codes and doing binary entropy on each component of that (Gemini suggested that again).

Well, this is it for now. I hope you have enjoyed the read! You can find the code on GitHub.